Matrix Algorithm in linear time

通常关于矩阵的算法，时间复杂度都是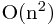，但是下面两个问题可以有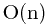的解法

1.这个问题是数据结构课的 story time 老师让思考的一个问题：

给定一个n*n的矩阵，矩阵中的每个元素都比它左边和上边所有的元素大，利用二分查找的思想判断矩阵中是否存在值K

大家很快说出从对角线上的元素开始判断，可是这样二分判断后，如果值不相等，得到一个L型的子矩阵，递归的过程无法继续，于是老师讲了下面这段话并说出答案：In designing a recursive algorithm, make sure you can repeat the strategy after the base case. 答案是从右上方的元素开始判断，伪代码如下：

Input: a matrix M with n rows and n columns, where M[i][k] < M[i][j], k < j and 
       M[k][j] < M[i][j], k < i. A given number K

Output: "yes", if number K is in the matrix; otherwise, "no"

binary_search_in_Matrix(int row, int column, int K)

if row > n or column < 0 then

return "no"

if K > M[i][j] then

binary_search_in_Matrix(row+1, column, K)

else if K < M[i][j] then

binary_search_in_Matrix(row, column-1, K)

else

return "yes"

最多2*n次基本操作，所以时间复杂度O(n)

2. 另一个相似的问题是《算法导论》上的作业，题目如下：

When an adjacency-matrix representation is used, most graph algorithms require time 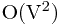, but there are some exceptions. Show that determining whether a directed graph G contains a "universal sink" - a vertex with in-degree |V| -1 and out-degree 0 - can be determined in time 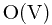, given an adjacency matrix of G.

算法伪代码如下：

Input: an adjacency matrix M of graph G

       an array named flag to remember whether a vertx is universal sink

Output: "yes", if G contains an "universal sink"; otherwise, return "no"

while i < n and j < n

do if M[i][j] == 1 then// i can't be universal sink

     i++

     flag[i] <-- false

     else // j can't be universal sink

     j++

     flag[j] <-- false

时间复杂度分析与上面的问题相似，为O(n)