最长递增子序列

一.问题描述

设 X = <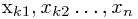>是n个不同的实数序列，L的递增子序列L'= <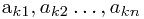>,其中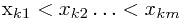, 求最大的m值

二.问题求解

2.1 转化为LCS问题求解

设序列A = <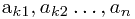>是序列 X = <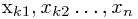>按递增顺序排好的序列，则A与L的最长公共子序列为L的最长递增子序列。这样把求最长递增子序列问题规约为最长公共子序列问题LCS了。

此解法的时间复杂度为：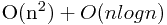

2.2 使用动态规划求解

设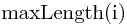为X中以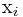为末元素的最长递增子序列的长度，有如下的递推方程：

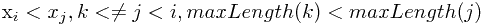
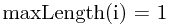
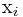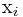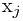即在求以为末元素的最长递增子序列长度时，对所有在前面的元素,且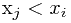,如果j的值存在，找出的最大值，则,否则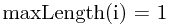

算法如下：

function lis_length( a )
    n := a.length
    q := new Array(n)
    for k from 0 to n:
        max := 0;
        for j from 0 to k, if a[k] > a[j]:
            if q[j] > max, then set max = q[j].
        q[k] := max + 1;
    max := 0
    for i from 0 to n:
        if q[i] > max, then set max = q[i].
    return max;

程序如下:

/*
**Descrition:	Returns the length of the longest increasing subsequence
**		Note that this is looking for the longest strictly increasing subsequence
**		This can be modified for other situations
**Author:	jia1546@163.com
**Date:		Oct 15, 2011
**Version:	1.0	
*/

#include <stdio.h>
#include <stdlib.h>

int lis(int *a, int n)
{
    int i, j;
    int *best, *prev;
    int max = 0;
    best = (int*)malloc(sizeof(int) * n);
    prev = (int*)malloc(sizeof(int) * n);

    for(i=0; i<n; i++)
    {
	best[i] = 1;
        prev[i] = i;
    }

    for(i=1; i<n; i++)
	for(j=0; j<i; j++)
 	    if(a[i] >= a[j] && best[i] < best[j] + 1)
	    {
		best[i] = best[j] + 1;
 		prev[i] = j;
	    }
    
    for(i=0; i<n; i++)
    	if(max < best[i])
	    max = best[i];

    free(best);
    free(prev);
    
    return max;
}

int main()
{
    int n;
    int *array;
    int i;
    while(scanf("%d",&n) != EOF)
    {
 	array = (int*)malloc(sizeof(int) * n);

	for(i=0; i<n; i++)
	    scanf("%d",array+i);
	printf("# of the lis is: %d\n", lis(array, n));
	
    }
    return 0;
}

时间复杂度: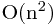 

2.2 改进的动态规划

在上一算法中，在计算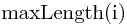时，需要找出最大的,由于无序，所以只能顺序查找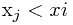的最大值,如果能让有序，可以使用二分查找的方法降低复杂度到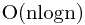

数组M[j]存储所有长度为j的子序列中最小末元素的X[k]的下标k

数组P[k]存储以X[k]为末元素的最长递增子序列中X[k]的前一元素的位置

算法如下：

L=0
for i=1,2,...n
    binary search for the largest positive j<=L
     such that X[M[j]] < X[i](or set j=0 if no such j exists)
    P[i] = M[j]
    if  j == L or X[i] < X[M[j+1]]
	M[j+1] = i
	L = max(L, j+1)

程序如下:

#include <vector>
using namespace std;
 
/* Finds longest strictly increasing subsequence. O(n log k) algorithm. */
void find_lis(vector<int> &a, vector<int> &b)
{
	vector<int> p(a.size());
	int u, v;
 
	if (a.empty()) return;
 
	b.push_back(0);
 
	for (size_t i = 1; i < a.size(); i++) 
        {
                // If next element a[i] is greater than last element of current longest subsequence a[b.back()], just push it at back of "b" and continue
		if (a[b.back()] < a[i]) 
                {
			p[i] = b.back();
			b.push_back(i);
			continue;
		}
 
                // Binary search to find the smallest element referenced by b which is just bigger than a[i]
                // Note : Binary search is performed on b (and not a). Size of b is always <=k and hence contributes O(log k) to complexity.    
		for (u = 0, v = b.size()-1; u < v;) 
                {
			int c = (u + v) / 2;
			if (a[b[c]] < a[i]) u=c+1; else v=c;
		}
 
                // Update b if new value is smaller then previously referenced value 
		if (a[i] < a[b[u]]) 
                {
			if (u > 0) p[i] = b[u-1];
			b[u] = i;
		}	
	}
 
	for (u = b.size(), v = b.back(); u--; v = p[v]) b[u] = v;
}
 
/* Example of usage: */
#include <cstdio>
int main()
{
	int a[] = { 1, 9, 3, 8, 11, 4, 5, 6, 4, 19, 7, 1, 7 };
	vector<int> seq(a, a+sizeof(a)/sizeof(a[0])); // seq : Input Vector
	vector<int> lis;                              // lis : Vector containing indexes of longest subsequence 
        find_lis(seq, lis);
 
        //Printing actual output 
	for (size_t i = 0; i < lis.size(); i++)
		printf("%d ", seq[lis[i]]);
        printf("\n");    
 
	return 0;
}

Ref

http://www.algorithmist.com/index.php/Longest_Increasing_Subsequence

http://en.wikipedia.org/wiki/Longest_increasing_subsequence