问题描述: 输入一组整数,求出这组数字子序列和中最大值
Jon Bentley’s在《编程珠玑》中给出的算法如下:
input: an array of integers
output: largest sum of contiguous integers in the given array A
Algorithm:
total = 0 // sum of contiguous integers
maxNow = 0 // the max sum up to the current position
for each element A[i] in the given array A
do total = max(total + A[i], total)
maxNow = max(maxNow, total)
output maxNow
time complexity : O(n)
这个算法最核心的思想在于:如果a[i]是负数那么它不可能代表最有序列的起点,因为任何包含a[i]的作为起点的子序列都可以通过用a[i+1]作为起点来改进。类似的有,任何的负的子序列不可能是最优子序列的前缀
但是这个算法存在问题:如果所有整数都是负数,则输出0,显然不对,这个情况下最大序列和应为数组中所有负数的最大值,所以修改原来的算法,加入判断。详细的C代码如下:
C代码如下:
#include <stdio.h>
#include <stdlib.h>
long long max(long a, long b)
{
long long result;
result = a > b ? a : b;
return result;
}
int main()
{
int n, i;
long long *array;
long long maxNow, total;
long long maxEle, allNegative;
while(scanf("%d", &n) != EOF)
{
array = (long long *) malloc(sizeof(long long) * n);
for(i=0; i<n; i++)
scanf("%lld", array+i);
maxNow = 0;
total = 0;
allNegative = 1;
maxEle = array[0];
for(i=0; i<n; i++)
{
total= max(total+array[i] , 0);
maxNow = max(maxNow, total);
maxEle = max(maxEle, array[i]);
if(array[i] >= 0)
allNegative = 0;
}
if(allNegative)
printf("%lld\n", maxEle);
else
printf("%lld\n", maxNow);
}
return 0;
}
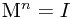
 ,使得M
,使得M 